
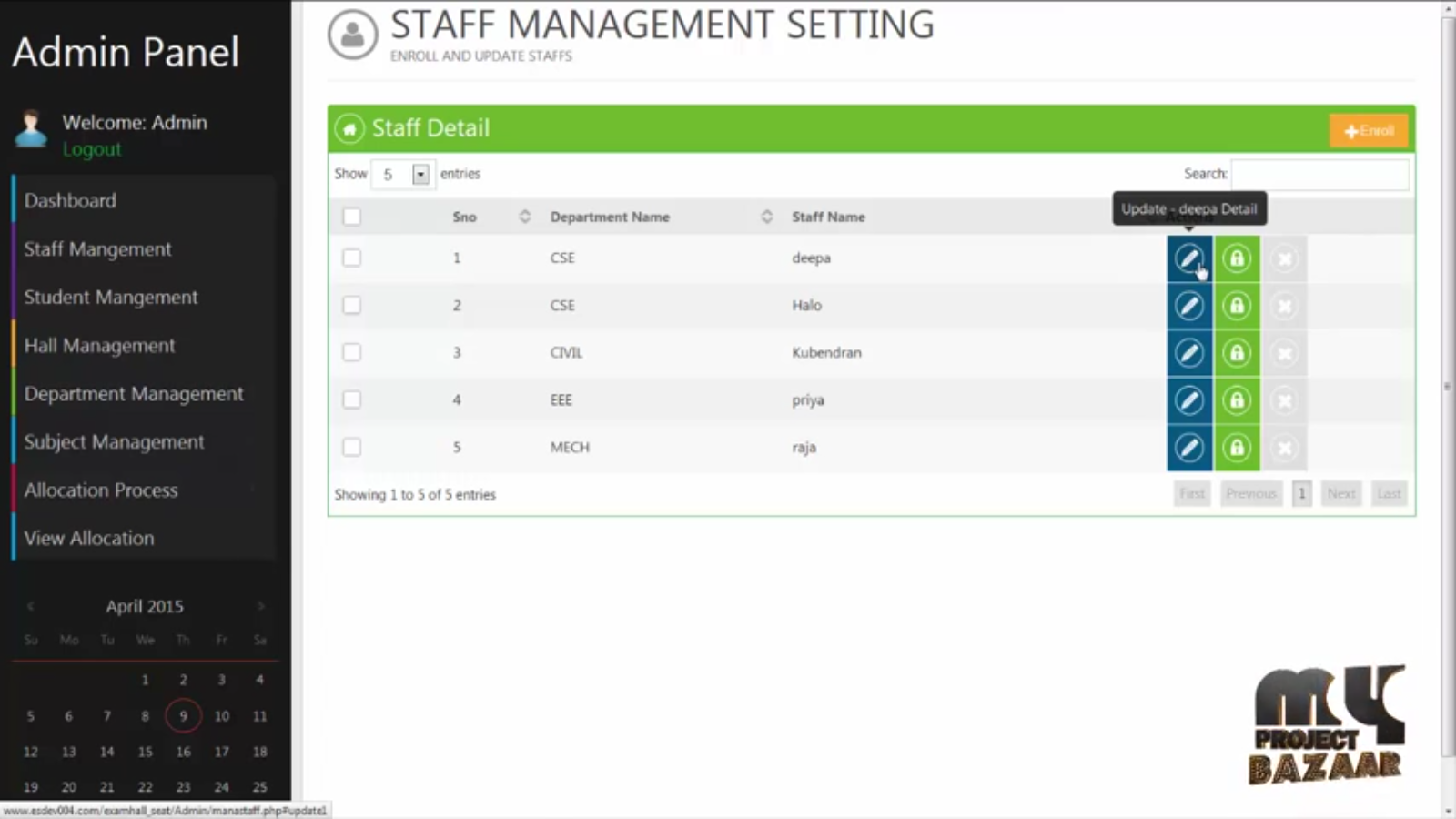
Exam hall Seat allocation process
Product Description
Abstract—The examination scheduling problem is a classical, old and famous problem in the field of optimization problems. Examination scheduling is an NP-Hard problem. In examination scheduling while considering No Room Splitting as a hard constraint, room allocation to exams can be treated as N-modified subset sum problem where N is the number of available rooms, given set is consisting of all available exams for scheduling and required sum is the seating capacity of the room for which scheduling is being carrying out in the current iteration. As classical subset sum problem, < Final Year Projects > it is an NP-Complete Problem. In our work this problem is solved by using multi-objective genetic algorithm with graph coloring and hence room allocation can be done in examination scheduling.
Including Packages
Our Specialization
Support Service
Statistical Report

satisfied customers
3,589
Freelance projects
983
sales on Site
11,021
developers
175+Additional Information
| Domains | |
|---|---|
| Programming Language |
Would you like to submit yours?















There are no reviews yet