A General Technique for Top-k Geometric Intersection Query Problems
Product Description
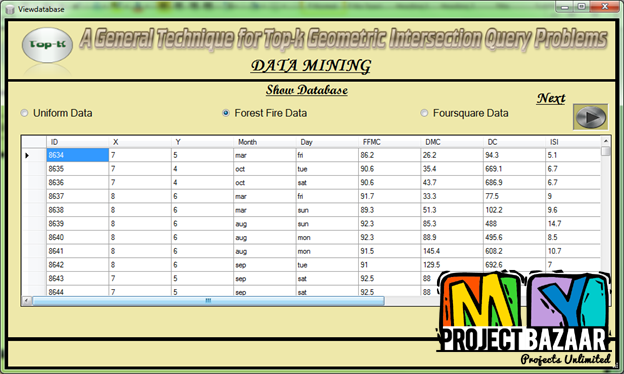
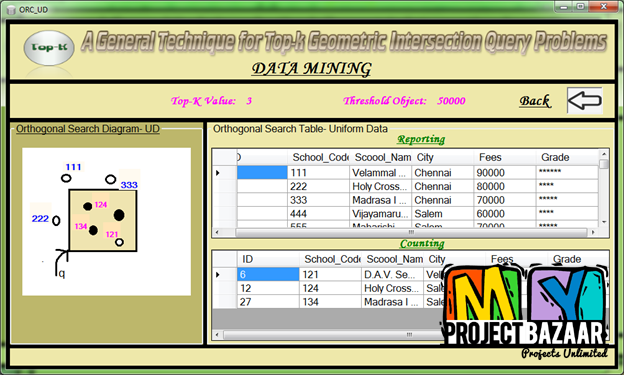
Abstract— A General Technique for Top-k Geometric Intersection Query Problems. In a top-k Geometric Intersection Query (top-k GIQ) problem, a set of n weighted, geometric objects in Rd is to be preprocessed into a compact data structure so that for any query geometric object, q, and integer k > 0, the k largest-weight objects intersected by q can be reported efficiently. While the top-k problem has been studied extensively for non-geometric problems (e.g., recommender systems), the geometric version has received little attention. This paper gives a general technique to solve any top-k GIQ problem efficiently. The technique relies only on the availability of an efficient solution for the underlying (non-top-k) GIQ problem, which is often the case. Using this, asymptotically efficient solutions are derived for several top-k GIQ problems, including top-k orthogonal and circular range search, < Final Year Projects > point enclosure search, halfspace range search, etc. Implementations of some of these solutions, using practical data structures, show that they are quite efficient in practice. This paper also does a formal investigation of the hardness of the top-k GIQ problem, which reveals interesting connections between the top-k GIQ problem and the underlying (non-top-k) GIQ problem.
Video
View Demo
Including Packages
Our Specialization
Support Service
Statistical Report
satisfied customers
3,589
Freelance projects
983
sales on Site
11,021
developers
175+
Additional Information
| Domains | |
|---|---|
| Programming Language |
Bluebird –
Hi this is kind of of off topic but I was wondering if blogs use WYSIWYG editors or if you have to manually code with HTML. I'm starting a blog soon but have no coding know-how so I wanted to get guidance from someone with experience. Any help would be enormously appreciated! https://cse.google.sh/url?q=https://www.podchaser.com/podcasts/credit-building-and-money-talk-1090314/episodes/how-instant-approval-credit-ca-57552233
visit –
I would like to voice my love for your generosity giving support to men and women that have the need for help with this particular area of interest. Your very own dedication to passing the message across has been remarkably helpful and have all the time allowed guys and women much like me to achieve their desired goals. Your personal invaluable guidelines implies this much to me and far more to my office colleagues. Regards; from all of us. http://images.google.co.bw/url?q=https://thetuckernews.com/what-are-the-advantages-of-a-mercury-card/
พนันบอล –
By doing long distance runs, you will increase your stamina on the field. https://live22center.com
คาสิโน –
ภาพงามเล่นง่ายได้เงินไวจำเป็นต้องยกให้ สล็อตออนไลน์เลยจ๊านะครับ พูดได้ว่าเป็นเกมยอดนิยมที่ครอบครองใจคนอีกหลายๆคนอย่างยิ่งจริงๆเว็บการพนันออนไลน์อันดับ 1 ก็เลยไม่พลาด จัดทั้งยังโบนัสแล้วก็แจ็คพอตแบบรัวๆเพื่อเพิ่มหนทางทำเงินให้สมาชิกนั่นเองครับ https://xn--42c6ad1bu8he2g.com
พนันบอล –
By doing this you will have a true interest in the things you are blogging about and this will reflect in your writing. https://batabet-sub.com
บาคาร่าออนไลน์ –
Choose a niche that you are passionate about. https://heng44.com
เกมส์คาสิโน –
By doing this, you are giving your readers relevant links, which can possibly generate additional revenue for you. https://gtrbet-bet.com
การพนันออนไลน์ –
By incorporating lean protein in your diet, you will help build strong healthy muscles that are required for kicking the ball accurately. https://maxbet-bet.com
ยูฟ่า –
หากคิดจะเล่นสล็อตออนไลน์ก็ต้องที่ เว็บการพนันออนไลน์อันดับ 1 เลยครับเพราะเว็บไซต์ของเราได้รวบรวมสล็อตไว้ทุกค่ายไม่เพียงเท่านั้นยังมีเกมอื่นๆอีกเพียบ ทั้งบาคาร่า แทงบอล ยิงปลา เรียกได้ว่ามีครบทุกเกมเลยล่ะครับ ไม่เพียงเท่านั้นยังเป็นเว็บไซต์ที่จ่ายจริงไม่มีโกง ฝากถอนไม่มีขั้นต่ำที่มาพร้อมระบบอัตโนมัติ https://gtrbetcenter.com
คาสิโนออนไลน์ –
แหล่งรวมเกมออนไลน์จำต้องยกให้ คาสิโนออนไลน์ มีครบจบที่ตรงนี้ที่เดียวครับ ทั้งยังบาคาร่า พนันบอล ที่สำคัญพลาดมิได้กับสล็อตออนไลน์ถือได้ว่าเกมยอดนิยมในยุคนี้เลยก็ว่าได้ เพราะว่าได้เงินง่าย ทำเงินได้จริง ทุนน้อยก็รวยได้ ยิ่งที่ สล็อตออนไลน์ บอกเลยแจ็คพอตจำนวนไม่ใช่น้อยมาย! https://laobet-news.com
ยูฟ่า –
It is important that your blog is easily readable. https://welcome-918kiss.com
บาคาร่าออนไลน์ –
To help you get these ideas you should visit forums other forums and blogs. https://fun88-sub.com
การพนันออนไลน์ –
สล็อตออนไลน์เกมออนไลน์ที่สร้างความบันเทิงให้ผู้เล่นได้อย่างดีเยี่ยมทั้งยังภาพแล้วก็เอฟเฟคสุดตระการตาทำให้ให้ขึ้นมาเป็นเกมยอดฮิตได้อย่างไม่ยากเย็น บาคาร่า ได้รวมรวมสล็อตทุกค่ายเอาไว้ภายในเว็บไซต์แล้วเป็นระเบียบ รอคอยให้ท่านเข้ามาสัมผัสความรื่นเริงใจที่มาพร้อมการผลิตรายได้ https://ufabetday.com
เกมส์คาสิโน –
If you are a beginner and you don't know much about soccer, the best way to learn a bit more is to watch some players in action. https://welcome-sexygame.com
พนันบอล –
ศูนย์รวมสล็อตออนไลน์ ที่คนไทยให้ความสนใจ รวมเกมคาสิโนออนไลน์ ที่คนไทยนิยมเล่น เล่น บนเว็บไซต์ที่น่าเชื่อถือ https://sexygamesub.com
บาคาร่า –
อยากดูบอลสด อยากแทงบอลออนไลน์ต้องที่ การพนันออนไลน์ เลยครับ สมัครง่าย เล่นง่าย ระบบเจ๋ง ที่สำคัญที่สุดเล่นแล้วได้เงินจริง ทำเงินได้จริง ในเว็บไซต์มีบริการเกมมากมาย ทั้งบาคาร่า สล็อต ยิงปลา เหมือนยกคาสิโนมาไว้ในเว็บไซต์เลยครับ https://ligaz-bet.com
พนันบอล –
To practice this, work with a partner. https://heng44.com
UFA –
For many bloggers, putting ads on their blog is the quickest and most reliable way to derive some profit from their efforts. https://sagame-news.com/sagame-news-2/
UFA –
ช่วงต้นผมว่าเว็บไหนก็เหมือนกัน เนื่องจากเข้าไปก็พบเกมเดิมๆแม้กระนั้นเอาเข้าจริงๆมันไม่เหมือนกันครับผม ยิ่งเว็บไซต์ไหนที่เวลาฝากถอนจำเป็นจะต้องผ่านพนักงานอันนี้ผมชิงชังสุดเลย เสียเวล่ำเวลา ส่วนตัวผมว่า บาคาร่า ดีสุดเลยจ๊ะครับผม เค้าใช้ระบบอัตโนมัติ https://fifabet999.com/E0B89AE0B8B2E0B884E0B8B2E0B8A3E0B988E0B8B2E0B8ADE0B8ADE0B899E0B984E0B8A5E0B899E0B98C/
คาสิโนออนไลน์ –
บาคาร่า แหล่งรวมพนันออนไลน์ที่ดีที่สุดในปัจจุบันนี้เลยก็ว่าได้ ด้วยระบบที่เป็นสากลและความมั่นคงด้านการเงินที่สูงจึงมั่นใจได้ว่าหากท่านเข้ามาร่วมเป็นสมาชิกกับเว็บไซต์ของเรา ท่านจะได้รับเงินจริงและไม่ต้องเป็นกังวลว่าจะโดนโกงเลย เว็บของเราได้รวบรวมเกมพนันออนไลน์ไว้มากมายรับรองท่านไม่ผิดหวังแน่นอน https://123goalsub.com/e0b980e0b8a7e0b987e0b89ae0b8a1e0b8b2e0b981e0b8a3e0b887e0b897e0b8b5e0b988e0b8aae0b8b8e0b894e0b884e0b8b2e0b8aae0b8b4e0b982e0b899e0b8ad-3/
UFA –
Yes, football is a sport that's played in all sorts of weather. https://allbet-bet.com/ufabet/
UFA –
สำหรับคนที่ต้องการหารายได้ที่บ้านวันนี้เราขอเสนอเว็บพนันออนไลน์ เว็บการพนันออนไลน์อันดับ 1 เว็บของเราคือเว็บคาสิโนออนไลน์ อันดับหนึ่ง มีแทงบอลออนไลน์ไว้ให้บริการ พร้อมเกมออนไลน์อีกหลากหลายเกมทั้ง สล็อต บาคาร่า ยิงปลา และอื่นๆอีกมากมาย มากกว่า 200 เกม https://batabetsub.com/e0b895e0b8b4e0b894e0b895e0b988e0b8ad/
UFA –
อยากมีรายได้แต่ไม่ได้อยากต้องการเดินทางไปไหน ต้องการมีรายได้แต่ไม่ได้อยากต้องการลงทุนเยอะมาก เนื่องจากยุคนี้เป็นสมัยที่ใครๆก็จำเป็นที่จะต้องเซพตนเอง เว็บพนัน ก็เลยได้เก็บรวบรวมเกมออนไลน์ไว้ล้นหลามเพื่อคุณได้ทำเงินสร้างรายได้แบบง่ายๆทั้งบาคาร่า แทงบอล สล็อต https://123goalwinbet.com/123goalwinbet-E0B89EE0B899E0B8B1E0B899E0B8ADE0B8ADE0B899E0B984E0B8A5E0B899E0B98C
UFA –
กระแสพนันออนไลน์ว่าแรงแล้ว ยังแรงไม่สู้โปรโมชั่นเด็ดๆที่ การพนันออนไลน์ ขยันเอาอกเอาใจสมาชิกมากครับ แล้วก็ชอบใจผมซะด้วย ไม่ใช่แค่เรื่องโปรโมชั่นครับ ผมถูกใจที่เค้ามีเกมให้เลือกมากมาย ทั้งพนันบอล บาคาร่า ยิงปลา สล็อต เกมใหม่ๆมีหมด https://bigwinbetcash.com/bigwinbetcash-e0b8aae0b8a1e0b8b1e0b884e0b8a3e0b8aae0b8b8e0b894e0b981e0b8aae0b899e0b887e0b988e0b8b2e0b8a2e0b894e0b8b2e0b8a2/
UFA –
เว็บการพนันออนไลน์อันดับ 1 เว็บคาสิโนออนไลน์ที่ได้รวบรวมทุกเกมพนันออนไลน์ทั้งหมดเอาไว้เพื่อสนองความต้องการของเหล่าสมาชิก และยังเลือกใช้ระบบที่ดีที่สุดเพื่อให้สมาชิกได้รับความสนุกสนานบันเทิงอย่างเต็มพิกัดไปพร้อมๆกับการทำเงินไปด้วย แบบไม่ต้องมีอุปสรรคใดๆ รวมถึงระบบหลังบ้านที่มีทีมงานคอยช่วยเหลือตลอด 24 ชั่วโมง https://918kisswinbet.com/E0B980E0B8A5E0B988E0B899E0B980E0B881E0B8A1-E0B8A5E0B887E0B897E0B8B8E0B899E0B899E0B989E0B8ADE0B8A2-E0B984E0B894E0B989E0B980E0B887E0B8B4
UFA –
แทงบอลออนไลน์ คาสิโนออนไลน์ที่ถูกกล่าวถึงมากที่สุดในตอนนี้เพราะเป็นเว็บที่ได้รับความนิยมสูงสุด มีเกมให้เล่นหลากหลาย จ่ายจริง จ่ายเต็ม แบบไม่มีกั๊ก สมัครง่าย ใช้ระบบฝากถอนอัตโนมัติ ไม่เพียงเท่านั้นยังมีทีมงานดูแลตลอด 24 ชั่วโมง https://allbet-news.com/allbet-news-2/
UFA –
Avoid being a blogger who offers no unique content on your blog. https://allbet-sub.com/E0B980E0B8A7E0B987E0B89AE0B89EE0B899E0B8B1E0B899E0B8ADE0B8ADE0B899E0B984E0B8A5E0B899E0B98CE0B896E0B8B9E0B881E0B881E0B88EE0B8ABE0B8A1
UFA –
To maximize your athletic potential, you need to be flexible and have a wide range of motion. https://918kiss-sub.com/918kiss-sub-4/
UFA –
แหล่งรวมเกมออนไลน์จะต้องชูให้ สล็อตออนไลน์ มีครบจบที่ตรงนี้ที่เดียวครับผม ทั้งบาคาร่า แทงบอล ที่สำคัญพลาดไม่ได้กับสล็อตออนไลน์ถือได้ว่าเกมยอดฮิตในยุคนี้เลยก็ว่าได้ ด้วยเหตุว่าได้เงินง่าย ทำเงินได้จริง ทุนน้อยก็มั่งมีได้ ยิ่งที่ การพนันออนไลน์ บอกเลยแจ็คพอตมากมายมาย! https://aloha6969.com/E0B980E0B8A7E0B987E0B89AE0B89EE0B899E0B8B1E0B899E0B8ADE0B8ADE0B899E0B984E0B8A5E0B899E0B98CE0B896E0B8B9E0B881E0B881E0B88EE0B8ABE0B8A1/
ยูฟ่า –
แทงบอลออนไลน์ สล็อตออนไลน์ และหวยออนไลน์ หากท่านต้องการใช้เวลาว่างให้เป็นประโยชน์และผ่อนคลายไปในเวลาเดียวกัน ท่านสามารถสมัคร สล็อตออนไลน์ เพื่อเล่นคาสิโนออนไลน์ได้อย่างตามใจชอบ https://918kiss-sub.com/918kiss-sub-3/
UFA –
If you want to better your skills so you can show off on the field, read on. https://918kiss-sub.com/ufa
Click here –
Hi there, i read your blog from time to time and i own a similar one and i was just wondering if you get a lot of spam responses? If so how do you stop it, any plugin or anything you can advise? I get so much lately it's driving me crazy so any support is very much appreciated. http://ukcgi.com/index.php/User:CeciliaCurrey
jetbluemastercard com activate –
Please let me know if you're looking for a author for your site. You have some really great posts and I believe I would be a good asset. If you ever want to take some of the load off, I'd love to write some articles for your blog in exchange for a link back to mine. Please blast me an e-mail if interested. Thank you! https://justpin.date/story.php?title=the-advantages-of-credit-cards-with-benefits#discuss
toloco massage gun reviews –
Hello there! Would you mind if I share your blog with my twitter group? There's a lot of people that I think would really enjoy your content. Please let me know. Many thanks https://modelfol.io/popupLinks.php?url=https://theintouchnews.com/2021-toloco-massage-gun-review-muscle-recovery-tool/
startwatch.own.tv/activate –
You could certainly see your expertise in the work you write. The arena hopes for even more passionate writers like you who aren't afraid to say how they believe. All the time follow your heart. https://doxoforo.com/index.php?title=Free_Of_Charge_On_Line_Online_Video_Clip_Web_Site_That_Are_Not_Basically_No_Charge..._Advice_No._23_Of_228
shorten link –
Wow, superb weblog structure! How long have you been blogging for? you made running a blog look easy. The total glance of your site is fantastic, as neatly as the content material!! https://shorte.top/
Social Media Marketing –
Wow, incredible weblog structure! How lengthy have you been blogging for? you make running a blog look easy. The full look of your web site is excellent, as well as the content!! https://shorte.top/90sp8
Affiliate Marketing –
Wow, awesome blog layout! How lengthy have you ever been blogging for? you made blogging glance easy. The total glance of your website is wonderful, as neatly as the content material!! https://shorte.top/90sp8
Jryghg –
Ileoao qrvrav how to buy stromectol - ivermectin 6mg dosage ivermectin price uk