Error Detection in Majority Logic Decoding of Euclidean Geometry Low Density Parity Check (EG-LDPC) Codes

Error Detection in Majority Logic Decoding of Euclidean Geometry Low Density Parity Check (EG-LDPC) Codes

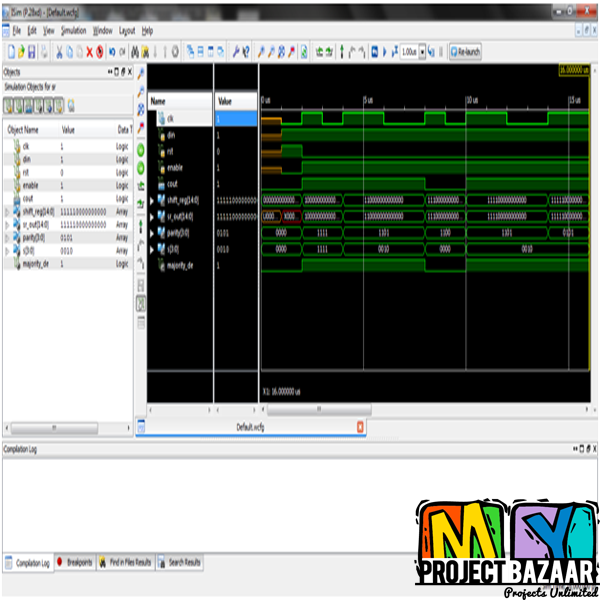
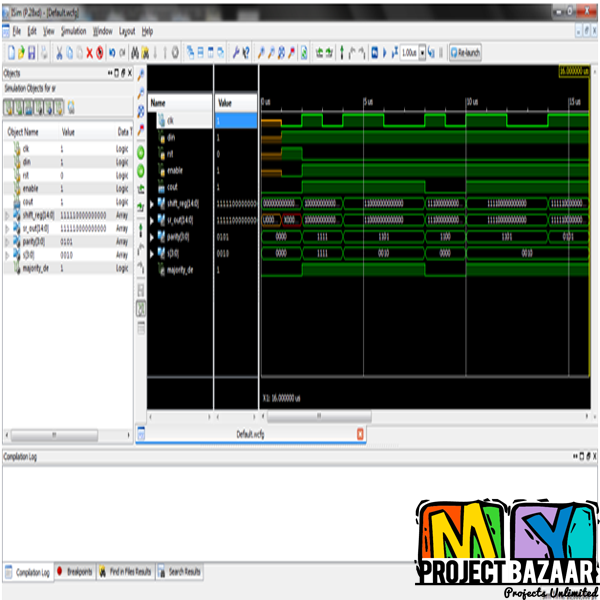
Abstract— Error Detection in Majority Logic Decoding of Euclidean Geometry Low Density Parity Check (EG-LDPC) Codes. In a recent paper, a method was proposed to accelerate the majority logic decoding of difference set low density parity check codes. This is useful as majority logic decoding can be implemented serially with simple hardware but requires a large decoding time. For memory applications, this increases the memory access time. The method detects whether a word has errors in the first iterations of majority logic decoding, < Final Year Projects > and when there are no errors the decoding ends without completing the rest of the iterations. Since most words in a memory will be error-free, the average decoding time is greatly reduced. In this brief, we study the application of a similar technique to a class of Euclidean geometry low density parity check (EG-LDPC) codes that are one step majority logic decodable. The results obtained show that the method is also effective for EG-LDPC codes. Extensive simulation results are given to accurately estimate the probability of error detection for different code sizes and numbers of errors.